Similarity Measures
2020-12-07
3 minutes
My favorite summary of cosine vs Euclidean distance metrics is that Euclidean distance focuses on the distance between two points whereas cosine distance focuses on the angle between two vectors.
Refresher on Cosine Similarity and Euclidean Distance
Cosine similarity is the dot product of two vectors divided by the product of the vector norms. It has a lower bound of -1 and and upper bound of 1.
np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
So for identical vectors you get a value of 1. For example,
A = [0,1,1]
B = [0,1,1]
np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
# 1.0
And for orthogonal vectors you get a value of -1. For example,
A = [0,1,1]
B = [0,-1,-1]
np.dot(A, B) / (np.linalg.norm(A) * np.linalg.norm(B))
# -1.0
Euclidean distance is calculated as the norm of the difference between two vectors. It has a lower bound of 0, but no upper bound.
np.norm(A-B)
For identical vectors you get a value of 0.
A = [0,1,1]
B = [0,1,1]
np.norm(A-B)
# 0.0
For these orthogonal vectors you get a value of 2.83. But the result will vary depending on how far the points described by the vectors are from one another.
A = [0,1,1]
B = [0,-1,-1]
np.norm(A-B)
# 2.83
What’s the difference?
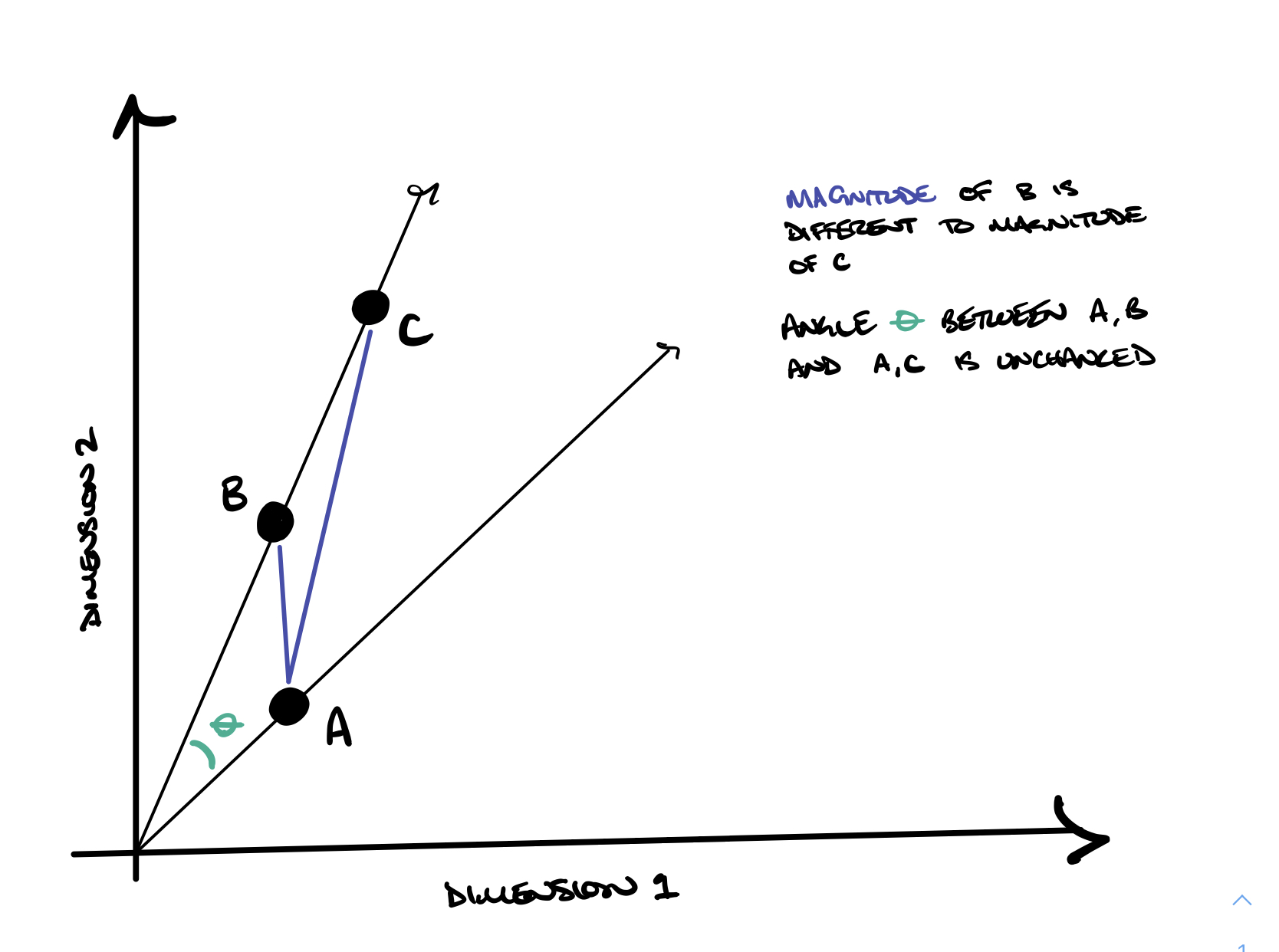
As an example consider the following vectors,
A = [0,1,1]
B = [0,2,1]
C = [0,6,3] # B*3
Between vector A and B we have the following distance calculations:
- Cosine: 0.95
- Euclidean: 1.0
Between vector A and C we have the following distance calculations:
- Cosine: 0.95
- Euclidean: 5.39
The similarity of vectors A and B have a comparable interpretation under both cosine similarity and Euclidean distance. That makes sense. The elements of each vector are identical.
However, the similarity between vector A and C differs depending on which calculation you use. The cosine similarity result is unchanged since vector C is just a scalar multiple of vector B (i.e. C points in the same direction as B). This makes sense since cosine similarity is based on the angle of the vectors; and the angle between A and B is the same as the angle between A and C.
Alternatively, the Euclidean distance calculation is different between A, B and A, C. Despite pointing in the same direction, the distance of the points described by each vector is different.
With this in mind, it’s preferred to use Euclidean distance when the magnitude for the vector matters and you don’t require your distance metric to have defined bounds, otherwise use cosine similarity. The figure below illustrates this result (note that vectors A, B, and C are arbitrary; they don’t map to the vectors defined above).
442 Words